Pitch Bend & Aftertouch

Adding pitch bending or aftertouch can add a lot of subtlety to an otherwise plain sounding midi region and help humanize it.

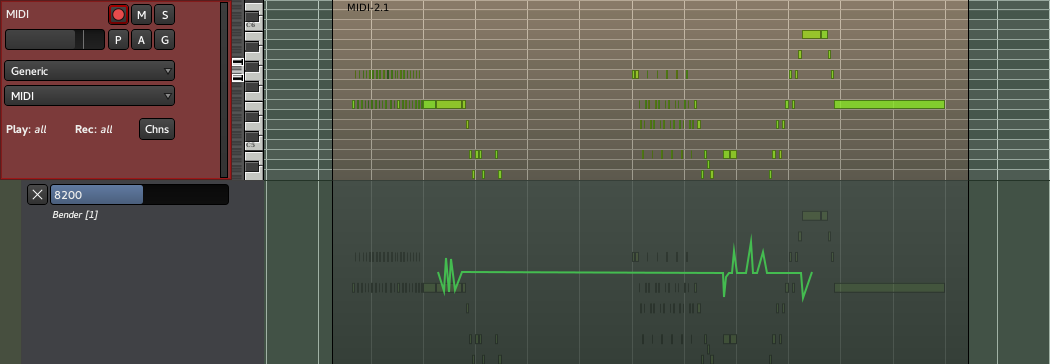
Pitch bending and aftertouch both work the same way, through automation, by right clicking the MIDI track's header > Automation > Bender (or Pressure) > the channel to bend.

Using the Draw tool, as for all the automations, allows to create a gradual change from one drawn point to another. A line in the center produces no change to the pitch, while a line above the center will bend the pitch to a higher note and a line going under the middle will bend the pitch to a lower note.

The pitch change depends on the synth-plugin used. Common ranges are an change of either ± 1, ± 2 or ± 4 semitones for the range 0 to 16383. The range is usually defined by the soundfont for each instrument. A value of 8192, which is also the default, means no pitch change.

Aftertouch works very similarly, though the values are between 0 and 127. It should be noted that aftertouch differs from velocity, as aftertouch allows to slightly change the timbre or create a vibrato, while the velocity sets the power with which the note is played (e.g. on a keyboard, the key is hit).